Blast Modelling

Towards a predictive model for the performance of commercial explosives in rock blasting

By Dr Gary J, Sharpe and Prof. Martin Braithwaite

Commercial or ammonium nitrate-based explosives (ANFOs, emulsions, slurries, and watergels) used in rock blasting applications, both in bulk and packaged applications, are ‘highly non-ideal’, that is to say they have the following characteristics: detonation velocity in applications much less than the ideal value; a curved detonation shock front; stable detonation only achievable in relatively large explosive charges; finite detonation reaction zone length.

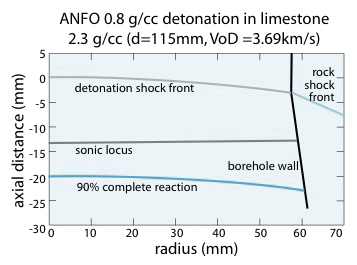
It is possible in principle to predict a priori the ideal detonation characteristics of such explosives given the formulation (ie explosive composition and initial density) via thermo- hydrodynamic chemical equilibrium codes with appropriate thermodynamic equations of state that describe the detonation products, including the ideal velocity of detonation (VoD), shock and post-detonation pressures etc. Unfortunately, in practical applications the detonation occurs under conditions far removed from this idealized scenario. The actual or non-ideal VoD, detonation pressures and ability of the explosive to do work on the rock are themselves complex functions of the charge size (eg borehole diameter) and the nature of the rock itself. Indeed, the explosive performance and the rock response are indelibly intertwined and cannot be unravelled. To illustrate this situation, figure 1 shows a schematic picture of a detonation in ANFO confined by a limestone.

The detonation shock front is curved due to the lateral expansion of the rock and an effective ‘driving zone’ bounded by a curved ‘sonic locus’ exists in which the energy release is markedly far from being complete. Hence, only the chemical energy in the subsonic region (or ‘detonation driving zone’) between the shock front and this sonic locus is available to drive the detonation forward. The remainder of the heat release occurs in the following supersonic expansion, but this is not communicated to the shock front. The problem is, therefore, intrinsically multi-dimensional and the VoD tends to be significantly less than the ideal value. The detonation shock, in turn, drives a shock into the rock, while the shocked borehole wall is pushed outwards by the high pressures generated in the detonation. The interaction of the rock and the explosive occurs via the explosive loading of the borehole wall and its response to this. This, in turn, leads to the strong coupling between the detonation characteristics (VoD, shock shape, pressures etc) and the movement and fracture of the rock. The critical or failure diameter is also a strong function of the rock type for a given explosive.

Hence, predicting the non-ideal detonation of commercial explosives is extremely challenging, especially in confined rock conditions. State-of-the art models which have been developed and are highly successful for weakly non-ideal military explosive applications, such as Detonation Shock Dynamics1, are unsatisfactory and problematic when applied to blasting with highly non-ideal commercial explosives. While it is, in principle, possible to simulate the coupled explosive-rock problem via finite volume/element/difference or discrete element-type methods2, this remains too computationally expensive to be of practical use due to the highly multi-scale nature of events (not to mention significant and unresolved numerical challenges of correctly capturing the very strong fluid-solid mechanics coupling). Fortunately, an entirely novel ‘variational streamline approach’ recently developed by the authors and co-workers3-4, via funding from the Engineering and Physical Sciences Research Council and industrial partners, represents a fundamental breakthrough in the ability to model and predict highly non-ideal detonation on a practical timescale with a single processor computer. These new variational methods provide approximate solutions to the problem which can then be iterated to arbitrary accuracy with very little computational cost. Even the simplest first approximation has been shown to be remarkably predictive of the final or exact solution3. The authors are currently developing these techniques into a quantitative non-ideal detonation software toolbox for the commercial explosives, mining and blasting industries via an EPSRC ‘Follow-on Fund’ project. In this article, the authors describe the progress and developments of this project, highlight the capabilities and potential applications of the models and discuss some of the difficult fundamental issues yet to be addressed in non-ideal detonation research.

Predicting velocity of detonation

The VoD of an explosive, in a given blasting scenario (rock type, borehole diameter etc) is currently used as the primary performance indicator. Since the ideal VoD cannot account for the strong influence of rock type, charge diameter etc, it is insufficient as a practical measure of commercial explosive performance. Hence, measurements of real VoDs are extremely important for commercial explosive performance characterization for rock blasting applications. VoDs can be measured both in the laboratory and in situ using various techniques, such as MREL’s continuous VoD recorders5. One of the key advantages of the authors’ non-ideal detonation models3-4 is that they are capable of providing near-instantaneous and accurate predictions of VoD as a function of explosive, rock and borehole diameter. Furthermore, they can also predict the confinement/rock- dependent critical diameter below which stable detonation cannot be achieved – an important factor not only for blast design but for safety issues. Hence, one major application of these models is as a method for predictively extrapolating any available (but in practice typically limited and proprietary) VoD data to different rock types and charge diameters.

Since these techniques are extremely computationally cheap – an entire ‘diameter effect’ of VoD as a function of charge size can be generated in around a second on a standard laptop – this makes auto-calibration of the burn or heat release rate of the explosive to any existing (unconfined, laboratory or field) VoD data feasible. It is to be noted that all non-ideal detonation models currently require some calibration of the explosive burn rate to measured data, due to the lack of first principles understanding of the complex burning mechanisms in highly heterogeneous explosives.

Figure 2 shows an example of the result of such a burn rate model parameter calibration using unconfined 0.8g/cc ANFO data from Sellers et al6. The ideal (infinite diameter) VoDs have been determined from the ideal detonation component of the model, which will form an integral part of the software package being developed. The authors’ thermodynamic (equation of state) models for non-ideal ANFO take into account the porosity (density) dependence of the shock response and use data from thermochemical calculations for the explosive products. The second example in figure 3 shows the calibration to unconfined emulsion data from Braithwaite et al7. In this case, no near-critical diameter data is given, so the failure diameter is a prediction of the model resulting from the calibration to the available data range.

Once the burn rate has been calibrated, the model can then be used to predict diameter effects in other confinements. The incorporation of the rock confinement effect requires some constitutive information about the rock, such as Hugoniot (shock response) data and elastic property measurements of the rock. Figure 4 shows the prediction by the model of the diameter effects in two different limestones and a sandstone using the ANFO 0.8g/cc model as calibrated above. Also shown are real VoD measurement data from the literature: 115mm borehole diameter limestone data and one 250mm datum for rock described as ‘felspathic sandstone’, both from Indian mines8 (rock density unknown); 165mm limestone data from Sellers et al6 (rock density unknown but described as ‘poor quality’);105mm and 125mm data from Mainadi & Robinson9 (limestone, no details given) and 250mm, 260mm and 300mm from Moxon et al10 (sandstone, no details given). Given the scatter on the data, the model can be seen to predict very well these field measurements.

It should be noted that no critical diameter is predicted for the higher-density limestone or the sandstones. This could be due to an assumption that the available Hugoniot data can be extrapolated linearly. For porous rocks the authors need to build in porosity effects on the Hugoniot at lower shock speeds/pressures. However, in general, for a given sufficiently strong confinement there will always be a critical VoD, below which the rock Hugoniot alone does not determine directly the confinement effect. This is related to situations where the VoD is dropping to near the rock sound speeds, whereby the ‘first approximation’ analysis of the rock response which was used to determine the degree of confining effect on the charge in figure 4 begins to break down.

Indeed, how to properly model situations where the in-situ VoD is similar to or less than the rock sound speeds is currently still an area requiring fundamental research. These scenarios, while rare in high-explosive applications, are commonly encountered in rock blasting by commercial explosives, in particular whenever hard rocks, such as granites or quartzites, are being blasted. Hence, in order to account for such effects, in parallel to the non-ideal model developments described here, the authors are also currently developing a highly efficient elastic-(visco)plastic wave mechanics model in partnership with Mantis Numerics Ltd, which, given the elastic and bulk properties of the rock, will specifically rapidly determine the confinement factor of the rock required by the non-ideal detonation models for all possible cases. Nevertheless, VoD measurement data remain vital in order to test/validate the resulting model predictions in these cases. However, an interesting, if perhaps overlooked, point is that while these situations of VoD comparable to confinement sound speeds can also occur in laboratory tests in which the explosive is confined in metal pipes, the thickness of the pipe then has a very large influence on the results10 and the results of such pipe tests are likely to be qualitatively different to confinement effect of an ‘infinite’ amount of rock. Hence, collection and analysis of significant amounts of in-situ field data for hard rocks remains essential.

Furthermore, when sufficient field VoD data is available, the data can be used as a known input into the model and the details of the corresponding rock response directly predicted. In fact, the model could then be used in ‘reverse’ to infer information about the rock itself and its confining effects, eg when the Hugoniot or elastic property data for the rock being blasted is sparse or not available, a calibrated explosive model and the VoD data could be used to infer information about the elastic-plastic shock response of the rock. In summary, the authors envisage that using the predictive capabilities of the non-ideal detonation model in tandem with VoD measurements would be highly advantageous.

Predicting explosive performance

While the (non-ideal) VoD is currently used as the primary performance indicator for commercial explosives and is used in several empirical concepts, such as ‘energy partitioning’, the VoD is itself the outcome of the complex interaction of the rock response and the non-ideal detonation and, perhaps counter-intuitively, it is not possible to relate directly the value of the VoD to the explosive performance, ie the impact of the explosive on the rock. For example, for a given explosive of fixed diameter, the highest (ideal) VoD would actually be achieved if the rock was completely unmoved by the detonation, while the minimum value would result from confinement by a weak rock which is both strongly shocked and strongly heaved by the explosion.

Hence, the non-ideal detonation models being developed are intended to predict not just the VoD but the entire details about the detonation and rock response, as illustrated by the model output in figure 1. Indeed, one question the models are intended to answer is not just ‘what is the VoD’ but ‘what does the VoD mean?’. In particular, since ultimately the rock response is a function of the explosive loading along the borehole wall, the authors believe it is this loading profile which will perhaps be the most important output from their non-ideal detonation models. Figure 5 shows an example illustration of predictions of the explosive pressure profile along the borehole wall for ANFO in two different borehole diameters in a limestone. Also included for comparison is the corresponding ideal detonation pressure profile, which helps to show more quantitatively the degree of non-ideality. Note that the rock sees a lower compressive stress loading along the wall from the smaller diameter charge due mainly to the lower VoD. Indeed, when the expansion of the borehole wall is large, the pressures (and temperature) drops most rapidly along it, such that the heat release/burning of the explosive near the wall region tends to take a very long time to reach completion and can even be quenched (ie again perhaps counter-intuitively at first, there is actually a correspondence between large response and movement of the rock with a low VoD and incomplete explosive energy release).

Explosive performance comparisons

Summarizing the above, the first-generation package will provide, for a given explosive formulation: ideal detonation characteristics as an essential starting point; rock- and diameter-dependent VoD and critical diameter predictions; entire solution of the non-ideal detonation of the explosive – in particular the pressure history along the borehole wall; and rock response information – shock and elastic wave strengths and speeds in the rock and the borehole wall movement. More importantly, however, this capability provides a quantitative means to compare these different performance indicators across different explosives. Indeed, at the start of the project, a survey/feedback questionnaire was sent out to industrial partners and interested parties to better understand how the software might be exploited. One of the main questions was: ‘Would you or your company support the idea of standardized explosive performance measures being used across the industry?’ Interestingly, the response to this was 100% positive. Hence, a major incentive in continued development of the software is actually as a provision of the industry standard for quantification of performance of explosive products which can be used equitably across the entire commercial explosives and blasting sectors.

As an illustrative example of this potential, figures 6 and 7 show preliminary results of a comparative study of the non-ideal detonation behaviour and corresponding rock response for two explosives (an ANFO and a bulk emulsion) with a medium-density limestone as the rock. Figure 6 shows the unconfined diameter effects of the two explosives. Note that the ANFO is more non-ideal in that the VoD drops much more quickly and further as the diameter decreases. The non-ideal detonation model predicts a larger failure diameter in the ANFO (68mm) as compared with the emulsion (44mm). Note also that the predicted steady VoD obtained for diameters at the detonation failure diameter is much lower in the ANFO (about 1km/s or 20% of the ideal VoD) compared to the emulsion (3.2km/s or 60% of the ideal VoD), again indicating the much more highly non-ideal nature of ANFO.

The limestone confinement diameter effects for the two explosives are also shown in figure 6. While the limestone has a relatively strong confining effect on the ANFO, increasing the VoD significantly above the unconfined value for a given charge diameter, it only very weakly confines the emulsion, ie the emulsion VoDs are predicted to be only slightly above the unconfined values in a given diameter and the critical diameter is only slightly smaller. Figures 1 and 7 show the non-ideal detonation configurations for the ANFO and the emulsion, respectively, for a given charge diameter of 115mm. Note the much more curved detonation shock front near the charge edge and the much steeper angle of the shock driven into the limestone for the emulsion case as compared with the ANFO, which serve to indicate the weaker confining effect of limestone on the emulsion. Note also the much smaller effective detonation reaction zone (the region between shock front, sonic locus and borehole wall) for the emulsion, which relates to the less non-ideal characteristics.

Figures 1 and 7 show that despite the significant differences between the ideal detonation characteristic and the different degrees of non-ideality of the detonation induced by rock on the two explosives, as well as the differences in the shock-wave propagation into the rock, the movement of the borehole wall (related to the heave effect on the rock) by the two explosives is predicted to be (fortuitously) very similar, at least for the same charge diameter of 115mm. This is further demonstrated in figure 8, which shows the pressure profiles along the borehole wall produced by the two explosives are very similar. However, since emulsions tend to be used in smaller diameter holes than ANFOs, a better ‘like-for-like’ comparison would be to compare the performance of the two explosives in different diameters. For example, figure 8 also compares the pressure profiles along the borehole wall for a larger-diameter (215mm) borehole filled with ANFO and a smaller-diameter borehole (85mm) filled with emulsion. The 215mm ANFO pressure profile now lies above the 85mm emulsion, even though the emulsion VoD remains higher.

The above example is mainly included to demonstrate that the interactions of non-ideal explosives with rock are very complex and very hard to predict a priori. The ideal detonation characteristics and/or measured or predicted non-ideal VoDs only provide a small piece of a complicated jigsaw of what happens when the detonation of a particular explosive in a particular diameter meets a particular rock. There is a very complicated interplay between VoD, expansion of the borehole wall (rock response), strength of shocks and waves driven into rock (peak pressures), explosive energy release rates and stress loading profile of the borehole wall. It is for precisely these reasons why a non-ideal detonation modelling capability which predicts more than VoD (ideal or non-ideal) is required in order to make proper ‘like-for-like’ comparisons of performance of different explosives in a given blasting scenario. Hopefully, the openly available software the authors are ultimately aiming to develop as the main deliverable of the project will not only provide a means for both explosives companies and users to undertake such studies, either together or independently, but also, due to the computational speed of the underlying methods, to be able to provide instant answers. Indeed, the authors currently envisage making the technology accessible via a web or phone app.

Blast optimization applications

Clearly, while there are many other potential applications of the stand-alone non-ideal detonation software toolbox under development, a more major impact would be through the incorporation of the outputs of the detonation models into larger-scale blast design or optimization models or codes. In other words, the detonation software is also intended to be available, and sufficiently versatile for easy incorporation, as a ‘sub-routine’ or interface with third party software. In particular, the authors have in mind the provision detonation ‘source terms’ (such as stress loading) required for full rock blasting models. Although outside the scope of the current EPSRC-funded project, as mentioned above the authors are currently developing in parallel very efficient rock wave mechanics software with Mantis Numerics Ltd for determination of the rock-dependent confinement effect on the explosive. However, by feeding back the explosive loading of the borehole wall from the non-ideal detonation model, the same wave mechanics software could be used to very rapidly compute the ‘near-field’ effect on the rock – ie predictions of the propagation of the various elastic-plastic waves driven into the rock by the explosive, the complete borehole wall deformation, crush zones of irreversible plastic deformation around the borehole etc. In turn, this ‘near-field’ rock response could be used as the starting point for larger-scale rock mechanics and fracture models.

SUMMARY

The interaction between commercial explosives and rock is significantly more complex than between high explosives and metals in military applications, due to the non-ideal nature of ammonium nitrate-based explosives as well as the complex heterogeneous nature of rock. Models or theories of the explosive performance in blasting applications need to account for the dependence of the velocity of detonation and, perhaps more importantly, the explosive loading of the rock, on the borehole diameter and on the nature of the rock itself, as well the explosive type, formulation, density etc. The authors are currently developing a non-ideal detonation software toolbox for the explosives, blasting and mining industries. The resulting technology is envisaged as a standardized methodology for evaluation and characterization of the performance of commercial explosives in blasting. It is based on novel variational streamline approaches which are capable of providing predictive solutions at minimal computational cost. Here, some preliminary results of this project have been presented, and the significant challenge of modelling commercial explosives discussed.

Requests for feedback and data

Please contact [email protected] with any feedback, suggestions or questions, or to be kept informed of the project’s progress. The authors would also welcome new project partners. Donations of laboratory or field data of commercial explosives, such as VoD measurements, to aid in the validation, testing and development of the models would also be very welcome.

Acknowledgements

This work is funded via the EPSRC Grant EP/J013218/1 ‘Predicting Detonation Characteristics and Performance of Commercial Explosives for the Mining and Explosive Manufacturing Industries’.

References

1. BDZIL, J.B., and S.D. STEWART: Annual Review of Fluid Mechanics, 39, 263, 2007.
2. SHARPE, G.J., and M. BRAITHWAITE: Journal of Engineering Mathematics, 53, 39, 2005.
3. WATT, S.D., et al: Journal of Engineering Mathematics, 75, 1, 2012.
4. SHARPE, G.J.: Industrial Short Course Lecture Notes, 2011, available on request.
5. MADSEN, A., and S. ROSE: Journal of Explosives Engineering, Jan-Feb 2008.
6. G. SELLERS, E., et al.: Proceedings of the 33rd Annual Conference on Explosives and Blasting Techniques, vol. 2, pp 1-11, 2007.
7. BRAITHWAITE, M., et al: in Rock Fragmentation by Blasting: Conference Proceedings of the 9th Int. Symp. on Rock Fragmentation by Blasting, pp. 237-333, 2009.
8. National Institute of Rock Mechanics, Project Code MT/96/96, Final Report 2001.
9. MAINADI, D., and P. ROBINSON: Explosives Engineering, Dec 1997.
10. MOXON, N.T., et al: Explosives Engineering, Dec 1992.

Dr Gary J. Sharpe PhD is Reader in Reactive Flows at the School of Mechanical Engineering, University of Leeds, and Prof. Martin Braithwaite BSc (Hons), AGGI PhD (Cantab), FRSC, FIChemE, CEng is academic visitor at the Laboratory for Scientific Computing, Cavendish Laboratory, Cambridge University, and visiting professor at Imperial College, London. This paper first appeared in Explosives Engineering, December 2012, published by The Institute of Explosives Engineers, and is reproduced here by kind permission.